REGRESIÓN
La regresión estadística o regresión a la media es la tendencia de una medición extrema a presentarse más cercana a la media en una segunda medición. La regresión se utiliza para predecir una medida basándonos en el conocimiento de otra.
MODELOS DE REGRESIÓN
En estadística la regresión lineal o ajuste lineal es un método matemático que modeliza la relación entre una variable dependiente Y, las variables independientes Xi y un término aleatorio ε. Este modelo puede ser expresado como:
 : variable dependiente, explicada o regresando.
: variable dependiente, explicada o regresando. : variables explicativas, independientes o regresores.
: variables explicativas, independientes o regresores.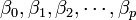 : parámetros, miden la influencia que las variables explicativas tienen sobre el regresando.
: parámetros, miden la influencia que las variables explicativas tienen sobre el regresando.
donde 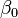 es la intersección o término "constante", las
es la intersección o término "constante", las  son los parámetros respectivos a cada variable independiente, y
son los parámetros respectivos a cada variable independiente, y  es el número de parámetros independientes a tener en cuenta en la regresión. La regresión lineal puede ser contrastada con la regresión no lineal.
es el número de parámetros independientes a tener en cuenta en la regresión. La regresión lineal puede ser contrastada con la regresión no lineal.
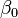 es la intersección o término "constante", las
es la intersección o término "constante", las  son los parámetros respectivos a cada variable independiente, y
son los parámetros respectivos a cada variable independiente, y  es el número de parámetros independientes a tener en cuenta en la regresión. La regresión lineal puede ser contrastada con la regresión no lineal.
es el número de parámetros independientes a tener en cuenta en la regresión. La regresión lineal puede ser contrastada con la regresión no lineal.
El modelo lineal relaciona la variable dependiente Y con K variables explicativas  (k = 1,...K), o cualquier transformación de éstas, que generan un hiperplano de parámetros
(k = 1,...K), o cualquier transformación de éstas, que generan un hiperplano de parámetros  desconocidos:
desconocidos:
 (k = 1,...K), o cualquier transformación de éstas, que generan un hiperplano de parámetros
(k = 1,...K), o cualquier transformación de éstas, que generan un hiperplano de parámetros  desconocidos:
desconocidos:
donde  es la perturbación aleatoria que recoge todos aquellos factores de la realidad no controlables u observables y que por tanto se asocian con el azar, y es la que confiere al modelo su carácter estocástico. En el caso más sencillo, con una sola variable explicativa, el hiperplano es una recta:
es la perturbación aleatoria que recoge todos aquellos factores de la realidad no controlables u observables y que por tanto se asocian con el azar, y es la que confiere al modelo su carácter estocástico. En el caso más sencillo, con una sola variable explicativa, el hiperplano es una recta:
 es la perturbación aleatoria que recoge todos aquellos factores de la realidad no controlables u observables y que por tanto se asocian con el azar, y es la que confiere al modelo su carácter estocástico. En el caso más sencillo, con una sola variable explicativa, el hiperplano es una recta:
es la perturbación aleatoria que recoge todos aquellos factores de la realidad no controlables u observables y que por tanto se asocian con el azar, y es la que confiere al modelo su carácter estocástico. En el caso más sencillo, con una sola variable explicativa, el hiperplano es una recta:
El problema de la regresión consiste en elegir unos valores determinados para los parámetros desconocidos  , de modo que la ecuación quede completamente especificada. Para ello se necesita un conjunto de observaciones. En una observación cualquiera i-ésima (i= 1,... I) se registra el comportamiento simultáneo de la variable dependiente y las variables explicativas (las perturbaciones aleatorias se suponen no observables).
, de modo que la ecuación quede completamente especificada. Para ello se necesita un conjunto de observaciones. En una observación cualquiera i-ésima (i= 1,... I) se registra el comportamiento simultáneo de la variable dependiente y las variables explicativas (las perturbaciones aleatorias se suponen no observables).
 , de modo que la ecuación quede completamente especificada. Para ello se necesita un conjunto de observaciones. En una observación cualquiera i-ésima (i= 1,... I) se registra el comportamiento simultáneo de la variable dependiente y las variables explicativas (las perturbaciones aleatorias se suponen no observables).
, de modo que la ecuación quede completamente especificada. Para ello se necesita un conjunto de observaciones. En una observación cualquiera i-ésima (i= 1,... I) se registra el comportamiento simultáneo de la variable dependiente y las variables explicativas (las perturbaciones aleatorias se suponen no observables).
Los valores escogidos como estimadores de los parámetros,  , son los coeficientes de regresión, sin que se pueda garantizar que coinciden con parámetros reales del proceso generador. Por tanto, en
, son los coeficientes de regresión, sin que se pueda garantizar que coinciden con parámetros reales del proceso generador. Por tanto, en
 , son los coeficientes de regresión, sin que se pueda garantizar que coinciden con parámetros reales del proceso generador. Por tanto, en
, son los coeficientes de regresión, sin que se pueda garantizar que coinciden con parámetros reales del proceso generador. Por tanto, en
Los valores 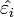 son por su parte estimaciones de la perturbación aleatoria o errores.
son por su parte estimaciones de la perturbación aleatoria o errores.
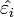 son por su parte estimaciones de la perturbación aleatoria o errores.
son por su parte estimaciones de la perturbación aleatoria o errores.
En estadística, la regresión no lineal es un problema de inferencia para un modelo tipo:
basado en datos multidimensionales  ,
, , donde
, donde 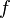 es alguna función no lineal respecto a algunos parámetros desconocidos θ. Como mínimo, se pretende obtener los valores de los parámetros asociados con la mejor curva de ajuste (habitualmente, con el método de los mínimos cuadrados). Con el fin de determinar si el modelo es adecuado, puede ser necesario utilizar conceptos de inferencia estadística tales como intervalos de confianza para los parámetros así como pruebas de bondad de ajuste.
es alguna función no lineal respecto a algunos parámetros desconocidos θ. Como mínimo, se pretende obtener los valores de los parámetros asociados con la mejor curva de ajuste (habitualmente, con el método de los mínimos cuadrados). Con el fin de determinar si el modelo es adecuado, puede ser necesario utilizar conceptos de inferencia estadística tales como intervalos de confianza para los parámetros así como pruebas de bondad de ajuste.
 ,
, , donde
, donde 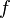 es alguna función no lineal respecto a algunos parámetros desconocidos θ. Como mínimo, se pretende obtener los valores de los parámetros asociados con la mejor curva de ajuste (habitualmente, con el método de los mínimos cuadrados). Con el fin de determinar si el modelo es adecuado, puede ser necesario utilizar conceptos de inferencia estadística tales como intervalos de confianza para los parámetros así como pruebas de bondad de ajuste.
es alguna función no lineal respecto a algunos parámetros desconocidos θ. Como mínimo, se pretende obtener los valores de los parámetros asociados con la mejor curva de ajuste (habitualmente, con el método de los mínimos cuadrados). Con el fin de determinar si el modelo es adecuado, puede ser necesario utilizar conceptos de inferencia estadística tales como intervalos de confianza para los parámetros así como pruebas de bondad de ajuste.
El objetivo de la regresión no lineal se puede clarificar al considerar el caso de la regresión polinomial, la cual es mejor no tratar como un caso de regresión no lineal. Cuando la función 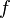 toma la forma:
toma la forma:
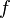 toma la forma:
toma la forma:
la función 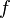 es no lineal en función de
es no lineal en función de  pero lineal en función de los parámetros desconocidos
pero lineal en función de los parámetros desconocidos  ,
,  , y
, y . Este es el sentido del término "lineal" en el contexto de la regresión estadística. Los procedimientos computacionales para la regresión polinomial son procedimientos de regresión lineal (múltiple), en este caso con dos variables predictoras
. Este es el sentido del término "lineal" en el contexto de la regresión estadística. Los procedimientos computacionales para la regresión polinomial son procedimientos de regresión lineal (múltiple), en este caso con dos variables predictoras  y
y 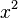 . Sin embargo, en ocasiones se sugiere que la regresión no lineal es necesaria para ajustar polinomios. Las consecuencias prácticas de esta mala interpretación conducen a que un procedimiento de optimización no lineal sea usado cuando en realidad hay una solución disponible en términos de regresión lineal. Paquetes (software) estadísticos consideran, por lo general, más alternativas de regresión lineal que de regresión no lineal en sus procedimientos.
. Sin embargo, en ocasiones se sugiere que la regresión no lineal es necesaria para ajustar polinomios. Las consecuencias prácticas de esta mala interpretación conducen a que un procedimiento de optimización no lineal sea usado cuando en realidad hay una solución disponible en términos de regresión lineal. Paquetes (software) estadísticos consideran, por lo general, más alternativas de regresión lineal que de regresión no lineal en sus procedimientos.
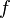 es no lineal en función de
es no lineal en función de  pero lineal en función de los parámetros desconocidos
pero lineal en función de los parámetros desconocidos  ,
,  , y
, y . Este es el sentido del término "lineal" en el contexto de la regresión estadística. Los procedimientos computacionales para la regresión polinomial son procedimientos de regresión lineal (múltiple), en este caso con dos variables predictoras
. Este es el sentido del término "lineal" en el contexto de la regresión estadística. Los procedimientos computacionales para la regresión polinomial son procedimientos de regresión lineal (múltiple), en este caso con dos variables predictoras  y
y 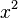 . Sin embargo, en ocasiones se sugiere que la regresión no lineal es necesaria para ajustar polinomios. Las consecuencias prácticas de esta mala interpretación conducen a que un procedimiento de optimización no lineal sea usado cuando en realidad hay una solución disponible en términos de regresión lineal. Paquetes (software) estadísticos consideran, por lo general, más alternativas de regresión lineal que de regresión no lineal en sus procedimientos.
. Sin embargo, en ocasiones se sugiere que la regresión no lineal es necesaria para ajustar polinomios. Las consecuencias prácticas de esta mala interpretación conducen a que un procedimiento de optimización no lineal sea usado cuando en realidad hay una solución disponible en términos de regresión lineal. Paquetes (software) estadísticos consideran, por lo general, más alternativas de regresión lineal que de regresión no lineal en sus procedimientos.
CORRELACIÓN
En probabilidad y estadística, la correlación indica la fuerza y la dirección de una relación lineal y proporcionalidad entre dos variables estadísticas. Se considera que dos variables cuantitativas están correlacionadas cuando los valores de una de ellas varían sistemáticamente con respecto a los valores homónimos de la otra: si tenemos dos variables (A y B) existe correlación si al aumentar los valores de A lo hacen también los de B y viceversa. La correlación entre dos variables no implica, por sí misma, ninguna relación de causalidad
Fuerza, sentido y forma de la correlación
La relación entre dos super variables cuantitativas queda representada mediante la línea de mejor ajuste, trazada a partir de la nube de puntos. Los principales componentes elementales de una línea de ajuste y, por lo tanto, de una correlación, son la fuerza, el sentido y la forma:
- La fuerza extrema según el caso, mide el grado en que la línea representa a la nube de puntos: si la nube es estrecha y alargada, se representa por una línea recta, lo que indica que la relación es fuerte; si la nube de puntos tiene una tendencia elíptica o circular, la relación es débil.
- El sentido mide la variación de los valores de B con respecto a A: si al crecer los valores de A lo hacen los de B, la relación es positiva; si al crecer los valores de A disminuyen los de B, la relación es negativa.
- La forma establece el tipo de línea que define el mejor ajuste: la línea recta, la curva monotónica o la curva no monotónica.
Distribución del coeficiente de correlación
El coeficiente de correlación muestral de una muestra es de hecho una varible aleatoria, eso significa que si repetimos un experimento o consideramos diferentes muestras se obtendrán valores diferentes y por tanto el coeficiente de correlación muestral calculado a partir de ellas tendrá valores ligeramente diferentes. Para muestras grandes la variación en dicho coeficiente será menor que para muestras pequeñas. R. A. Fisher fue el primero en determinar la distribución de probabilidad para el coeficiente de correlación.
Si las dos variables aleatorias que trata de relacionarse proceden de una distribución gaussiana bivariante entonces el coeficiente de correlación r sigue una distribución de probabilidad dada por:12
donde:
 es la distribución gamma
es la distribución gamma es la función gaussiana hipergeométrica.
es la función gaussiana hipergeométrica.
Nótese que 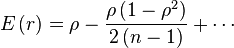 , por tanto r es estimador sesgado de
, por tanto r es estimador sesgado de  .
.
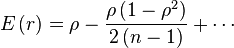 , por tanto r es estimador sesgado de
, por tanto r es estimador sesgado de  .
.
Puede obtenerse un estimador aproximado no sesgado resolviendo la ecuación:
for
Aunque, la solucón:
es subóptima. Se puede obtener un estimador sesgado con mínima varianza para grandes valores de n, con sesgo de orden  buscando el máximo de la expresión:
buscando el máximo de la expresión:
 buscando el máximo de la expresión:
buscando el máximo de la expresión:, i.e.
En el caso especial de que  , la distribución original puede ser reescrita como:
, la distribución original puede ser reescrita como:
 , la distribución original puede ser reescrita como:
, la distribución original puede ser reescrita como:
donde  es la función beta.
es la función beta.
 es la función beta.
es la función beta.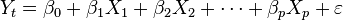







![\breve{\rho} = r \left[1 + \frac{1 - r^2}{2\left(n - 1\right)}\right]](http://upload.wikimedia.org/wikipedia/es/math/5/4/9/54905cbd515c2e553bf8eff42d36f479.png)
![\hat{\rho} = r \left[1 - \frac{1 - r^2}{2\left(n - 1\right)}\right]](http://upload.wikimedia.org/wikipedia/es/math/e/8/2/e82e9da1b00c5ea6a22c8e6c35ed0a22.png)

Buena información :)
ResponderEliminarMuchas gracias
ResponderEliminarMe ayudo mucho gracias por la información.
ResponderEliminarQue buena información, gracias <3
ResponderEliminar